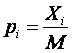
Рассмотрим процедуру вычисления θi и βj из эмпирических данных. В качестве исходных данных возьмем бинарную матрицу из таблицы 3.2.5. Дальнейшие расчеты выполним, следуя М.Челышковой6.
Сначала необходимо вычислить доли верных pi и неверных qi=1- pi ответов испытуемых.
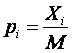
где Xi - индивидуальный балл испытуемого, M - количество заданий в тесте.
Например, для 2-го испытуемого имеем
![]()
q2 = 1 - p2 = 1 - 0,75 = 0,25.
Далее вычисляем начальные значения уровня подготовленности испытуемых по формуле
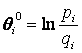
Для 2-го испытуемого имеем
![]()
Аналогичные расчеты выполняются для всех десяти испытуемых (таблица 3.2.5) и заносятся в таблицу 5.3.1.
Далее вычисляем начальное значение трудности заданий βj.

Здесь j пробегает значения от 1 до M, где M -количество испытуемых. В качестве примера рассчитаем начальное значение трудности 2-го задания. Величины pj и qj рассчитаны нами ранее и приведены в таблице 3.2.5.
![]()
Таблица 5.3.1. Начальные значения уровня
подготовленности испытуемых
|
i |
Xi |
pi |
qi |
qi0 |
(qi0)2 |
|---|---|---|---|---|---|
|
1 |
7 |
0,875 |
0,125 |
1,946 |
3,786 |
|
2 |
6 |
0,750 |
0,250 |
1,099 |
1,207 |
|
3 |
6 |
0,750 |
0,250 |
1,099 |
1,207 |
|
4 |
6 |
0,750 |
0,250 |
1,099 |
1,207 |
|
5 |
4 |
0,500 |
0,500 |
0,000 |
0 |
|
6 |
3 |
0,375 |
0,625 |
-0,511 |
0,261 |
|
7 |
2 |
0,250 |
0,750 |
-1,099 |
1,207 |
|
8 |
2 |
0,250 |
0,750 |
-1,099 |
1,207 |
|
9 |
1 |
0,125 |
0,875 |
-1,946 |
3,786 |
|
10 |
1 |
0,125 |
0,875 |
-1,946 |
3,786 |
|
|
|
|
|
å (qi0)2 = |
17,655 |
Расчеты для всех восьми заданий сведены в таблицу 5.3.2.
Таблица 5.3.2. Начальные значения трудности заданий
|
j |
Rj |
pi |
qi |
bj0 |
(bj0)2 |
|---|---|---|---|---|---|
|
1 |
7 |
0,700 |
0,300 |
-0,847 |
0,718 |
|
2 |
7 |
0,700 |
0,300 |
-0,847 |
0,718 |
|
3 |
6 |
0,600 |
0,400 |
-0,405 |
0,164 |
|
4 |
5 |
0,500 |
0,500 |
0,000 |
0 |
|
5 |
5 |
0,500 |
0,500 |
0,000 |
0 |
|
6 |
4 |
0,400 |
0,600 |
0,405 |
0,164 |
|
7 |
2 |
0,200 |
0,800 |
1,386 |
1,922 |
|
8 |
1 |
0,100 |
0,900 |
2,197 |
4,828 |
|
|
|
|
|
å (bj0)2 = |
8,514 |
Теперь мы можем вычислить средние значения уровня подготовленности испытуемых и трудности заданий.
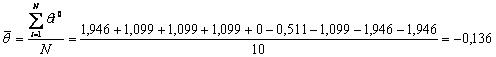
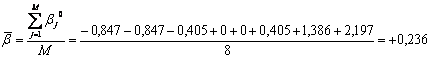
В таблицах 5.3.1. и 5.3.2 мы имеем значения параметров на разных интервальных шкалах. Нам надо свести их в единую шкалу стандартных оценок. Для этого необходимо вычислить дисперсии Sθ и Sβ, используя данные из таблиц 5.3.1 и 5.3.2.


Далее вычисляем угловые коэффициенты
![]()
![]()
Наконец, мы можем записать оценки параметров θ и β на единой интервальной шкале10.
![]()
![]()
Для нашего примера получим
θi = 1,911·θi0 + 0,236
βj=2,284· βj0 - 0,136
Все результаты сведены в таблицы 5.3.3 и 5.3.4 (второй столбец).
Из таблицы 5.3.4. следует, что
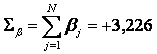
То есть, заданий с положительными βj больше, чем с отрицательными. Данный тест не сбалансированный, он содержит больше трудных заданий, чем легких.
Рекомендуется стремиться к тому, чтобы Σβ было близко к нулю.
Нам осталось вычислить стандартные ошибки измерения SE(θi) и SE(βj) для θi. и βj
|
Таблица 5.3.3. Расчетные параметры для уровня подготовленности испытуемых |
|||
|---|---|---|---|
|
i |
θi |
SE(θi) |
θi’ |
|
1 |
3,955 |
2,043 |
2,436 |
|
2 |
2,335 |
1,560 |
1,365 |
|
3 |
2,335 |
1,560 |
1,365 |
|
4 |
2,335 |
1,560 |
0,523 |
|
5 |
0,236 |
1,351 |
-0,157 |
|
6 |
-0,740 |
1,396 |
-0,781 |
|
7 |
-1,863 |
1,560 |
-1,431 |
|
8 |
-1,863 |
1,560 |
-1,431 |
|
9 |
-3,483 |
2,043 |
-2,217 |
|
10 |
-3,483 |
2,043 |
-2,217 |
|
Таблица 5.3.4. Расчетные параметры для
трудности |
|||
|---|---|---|---|
|
j |
βj |
SE(βj) |
βj’ |
|
1 |
-2,071 |
1,576 |
-1,545 |
|
2 |
-2,071 |
1,576 |
-1,669 |
|
3 |
-1,062 |
1,474 |
-0,603 |
|
4 |
-0,136 |
1,445 |
-0,502 |
|
5 |
-0,136 |
1,445 |
-0,256 |
|
6 |
0,790 |
1,474 |
0,102 |
|
7 |
3,030 |
1,806 |
1,854 |
|
8 |
4,882 |
2,408 |
2,620 |
![]()
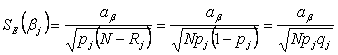
Например, для первого испытуемого получим
![]()
Для первого задания стандартная ошибка равна
![]()
Вычисленные значения стандартных ошибок приведены в таблицах 5.3.3 и 5.3.4 (третий столбец).