В качестве математической модели, связывающей успех испытуемого с уровнем его подготовленности и трудностью задания выбирается логистическая функция. Для модели Раша она имеет вид
![]() (5.2.1)
(5.2.1)
![]() (5.2.2)
(5.2.2)
Масштабный множитель 1,7 используется для совместимости модели G.Rasch с моделью A.Fergusson, где вероятность правильного ответа на задание выражена интегралом нормального распределения (5.2.3), что позволяет использовать вместо логистических кривых хорошо изученную интегральную функцию нормированного нормального распределения7
 (5.2.3)
(5.2.3)
Модель Раша носит название «1 Parametric Logistic Latent Trait Model» (1PL), а модель A.Fergusson - «1 Parametric Normal Ogive Model» (1PN). Поскольку модель Раша описывает вероятность успеха испытуемого как функцию одного параметра (θi - βj), то иногда ее называют однопараметрической моделью IRT.
Взаимодействие двух множеств θi и βj образует данные, обладающие свойством «совместной аддитивности» (conjoint additivity). Правильное использование модели Раша позволяет отделить оценки испытуемых от оценок трудности заданий и наоборот. Это свойство Rasch Measurement носит название separability parameter estimates8 - «независимость оценок заданий от испытуемых и оценок испытуемых от параметров заданий».
На рис.5.2.1. показаны три характеристические кривые согласно уравнению (5.2.1) с трудностями заданий -2, 0 и +2 логита (первое самое легкое, второе - среднее, третье самое трудное). Из приведенных зависимостей видно, что чем выше уровень
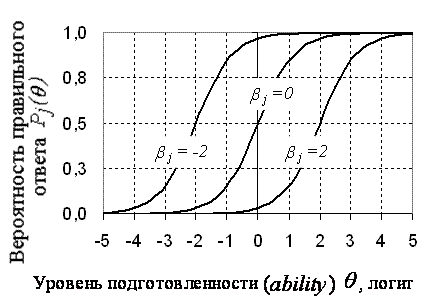
Рис.5.2.1. Характеристические кривые заданий (ICC) в модели (1PL).
подготовленности θ испытуемого, тем выше вероятность успеха в том или ином задании. Например, для испытуемого с θ =0 вероятность правильно ответить на первое задание близка к единице, на второе равна 1/2 и на третье почти равна нулю. Отметим, что в точках, где θ = β вероятность правильного ответа равна 0,5. То есть, если трудность задания равна уровню подготовленности (ability) испытуемого, то он с равной вероятностью может справиться или не справиться с этим заданием.
Характеристические (логистические) кривые для заданий теста в англо-язычной литература называются Item Characteristic Curve (ICC).
На рис.5.2.2. показаны три характеристические кривые испытуемых согласно уравнению (5.2.2) - «Person Characteristic Curve» (PCC). Показаны графики для трех испытуемых с уровнем подготовленности -2 логита (самый слабый), 0 логитов (средний) и +2 логита (сильный испытуемый).
Из приведенных зависимостей видно, что чем выше уровень подготовленности, тем выше вероятность правильного ответа на задание. Например, задание с трудностью b = 0 первый испытуемый ( q=-2) практически не сможет выполнить, второй q = 0) имеет вероятность выполнения задания равную 0,5, третий q=+2) легко справится с заданием, так как для него вероятность успеха почти равна единице.

Рис.5.2.2. Характеристические кривые испытуемых (PCC) в модели 1PL.
ДВУХПАРАМЕТРИЧЕСКАЯ МОДЕЛЬ БИРНБАУМА
Как видно из приведенных зависимостей, крутизна характеристических кривых в области Pj=0,5 одинакова, то есть дифференцирующая способность является константой. Для дихотомической модели эта константа равна 0,25.
Если тест содержит задания с различной дифференцирующей способностью, то однопараметрическая модель 1PL не может описать такие эмпирические данные. Для преодоления этой трудности А.Бирнбаум (A.Birnbaum)9 ввел еще один параметр - a (item discrimination parameter).
![]() (5.2.4)
(5.2.4)
 (5.2.5)
(5.2.5)
Параметр aj определеяет наклон (крутизну) характеристической кривой j-го заданий. Примеры характеристических кривых показаны на рис.5.2.3. Видно, что чем больше aj тем круче идет кривая, тем выше дифференцирующая способность задания.

Рис.5.2.3. ICC в двухпараметрической модели 2PL
Для еще лучшего соответствия эмпирическим данным А.Бирнбаум ввел третий параметр c - параметр угадывания*.
![]() (5.2.6)
(5.2.6)
 (5.2.7)
(5.2.7)
Из уравнений (5.2.5) и (5.2.6) видно, что при cj=0 и aj=1 эти уравнения переходят в однопараметрическую модель. По этой причине иногда говорят, что модель Раша является частным случаем двух и трехпараметрической моделей Бирнбаума. Формально это так, но по существу это неверно. К обсуждению этой проблемы мы вернемся далее.
На рис.5.2.4. приведены примеры характеристических кривых для трех заданий с трудностью β = 1, дискриминационным параметром aj = 1 и различными параметрами угадывания cj = 0, cj = 0,25, cj = 0,5.
Из приведенных графиков видно, что наличие параметра угадывания приводит к пропорциональному смещению ICC вверх на величину cj.
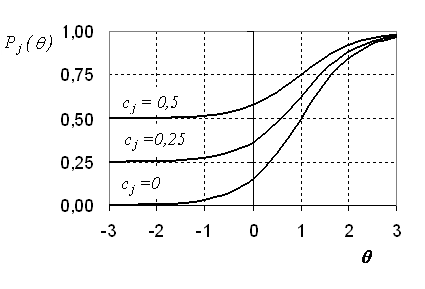
Рис.5.2.4. ICC в трехпараметрической модели 3PL,
αj=1, βj=1.
В качестве теоретической оценки cj можно использовать обратную величину от количества ответов в заданиях с выбором. Например, в тесте используются задания с четырьмя ответами, тогда cj = 1/4 = 0,25. Это значение должно уточняться при анализе эмпирических данных.
МОДЕЛЬ RASCH MEASUREMENT
Обсудим вопрос о степени пригодности моделей IRT для целей измерения латентных параметров.
Характерной особенностью модели Раша является то, что характеристические кривые (ICC) не пересекаются (рис.5.2.1). Это означает, что если некоторое задание «А» легче задания «Б», то это соотношение сохраняется во всем интервале изменения θ.
Совершенно иная картина наблюдается для двух- и трехпараметрической моделей. На рис.5.2.3 это хорошо видно. Задание с αj = 0,5 в области положительных значений θ является самым трудным из представленных трех заданий, то есть вероятность правильного ответа на это задание самая низкая. В области же отрицательных значений q это же задание теперь уже самое легкое - вероятность правильного ответа на него наибольшая. Получается, что для слабых учащихся это самое легкое задание, а для сильных учащихся - самое трудное.
Аналогичная картина наблюдается и для трехпараметрической модели. На рис.5.2.4. показан редкий случай непересекающихся характеристических кривых, так как для них выбраны одинаковые параметры βj=1 и αj=1, то есть все три задания имеют одинаковую трудность и одинаковый параметр дифференцирующей способности.
На рис.5.2.5 приведен другой пример.
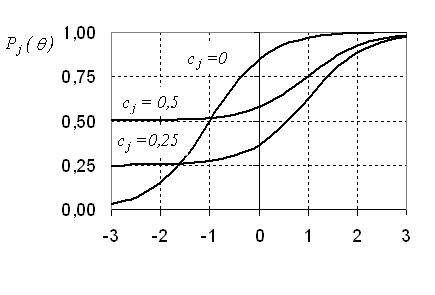
Рис.5.2.5. Пересекающиеся ICC в трехпараметрической модели.
Здесь у задания с параметром cj=0 изменена трудность βj= -1, что немедленно вызвало пересечение характеристических кривых. Задание с cj=0 в области θ < -2 является самым трудным. В области -1,5 < θ < -1 это задание легче задания с cj=0,25 и труднее задания с cj=0,5. В области θ > -1 задание с cj=0 является самым легким.
Подобное пересечение ICC практически всегда происходит для двух- и трехпараметрической моделей.
Таким образом, только однопараметрическая модель Раша соответствует требованиям, предъявляемым к качественному измерительному инструментарию. Именно модель RASCH MEASUREMENT больше всего пригодна для построения теста, как измерительного инструмента.
* В.Аванесов отмечает, что F.Lord называл cj параметром псевдоугадывания. Это указывает на то, что в величину cj дают вклад и другие факторы, помимо угадывания.